円周率計算のアルゴリズム

[ いろいろな開発環境に戻る ]

円周率を求めるアルゴリズムについて考える前に、念のため円周率について復習してみましょう。
円の面積の公式は：

S1 = πr²

です。この時の定数πのことを円周率というわけです。
もう一つ式を挙げましょう。正方形の面積は：

S2 = r²

です。この二つの式を比べると、半径がある長さである円の面積は、一辺が同じ長さの正方形の面積のπ倍であることがわかります。

それでは、早速円周率を求める方法を考えてみましょう。

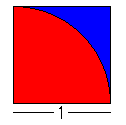
一辺の長さ1の正方形と半径1の円（扇形）が図のように配置されているとします。正方形の面積は1です。一方、扇形の中心角は正方形の一つの角と重なっていることから90度になりますから、扇形の面積はπ/4です。すなわち面積比は、1 : π/4になります。
この正方形の中にランダムに点を打つとします。それをたくさん繰り返すと、点の総数（青と赤の部分に打たれた点の合計）と扇形の中に含まれる点の数（赤い部分に入っている点の数）との比は、確率的に面積比に等しい1 : π/4に近づくはずです。
つまり、

点の総数 : 扇型の中の点の数 = 1 : π/4

となるはずです。この式の形を変えると、

π = (扇型の中の点の数 / 点の総数) × 4

となります。これはまさに円周率を求めるための式になっているわけです。

以上が円周率を求めるためのアルゴリズムです。円周率の計算には他にもいくつかの方法があり、ここで紹介したやり方は乱数に頼っているため最も精度が悪いものです。しかしながら「点を打ってその位置を調べるだけ」という、非常に簡単な処理で円周率が求められます。今回は開発環境の比較をするために簡単なサンプルを用意するのが目的なので、このアルゴリズムを採用しました。

瀬尾佳隆 (webmaster@seosoft.net)